Imaginen que en un cierto momento están con un grupo de personas, por ejemplo en una reunión familiar o en un bar, cualquier grupo aleatorio de personas valdría. Digamos que hay 25 personas. Les planteo la siguiente cuestión: ¿cuál creen que es la probabilidad de que en ese grupo de personas haya dos personas que cumplen los años el mismo día del mismo mes??
Pues la cosa es que ni mucho menos es pequeña. Vamos con lo que podríamos considerar el enunciado de la paradoja:
En una reunión de 23 personas escogidas aleatoriamente, la probabilidad de que dos de ellas cumplan los años el mismo día del mismo mes es de 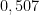 , es decir, hay un
, es decir, hay un 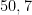 % de posibilidades de que haya dos personas que cumplan los años el mismo día del mismo mes.
% de posibilidades de que haya dos personas que cumplan los años el mismo día del mismo mes.
Para las 25 personas de mi ejemplo la probabilidad es aproximadamente de 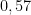 , es decir, casi el
, es decir, casi el 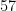 %.
%.
Básicamente lo que nos dice este resultado es que en una reunión de 23 o más personas es más sorprendente que no haya dos que coincidan en cumpleaños que el hecho de que sí las haya, algo que todo el mundo tiende a no creer en un primer momento.
Y la cosa mejora si aumentamos un poco más el número de personas del grupo. Les dejo unos cuantos resultados: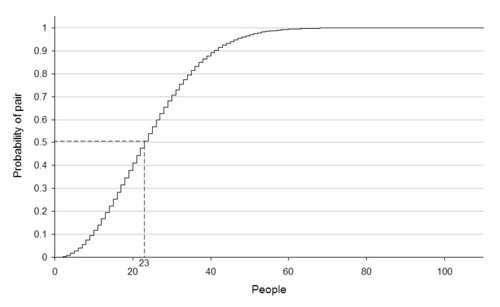
Para 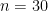 , la probabilidad es de
, la probabilidad es de 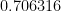 , poco más del
, poco más del 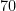 %.
%.
Para 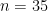 , la probabilidad es de
, la probabilidad es de 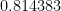 , poco más del
, poco más del 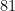 %.
%.
Para 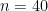 , la probabilidad es de
, la probabilidad es de 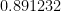 , casi del
, casi del 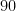 %.
%.
Para 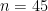 , la probabilidad es de
, la probabilidad es de 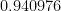 , cerca del
, cerca del  %.
%.
Para 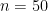 , la probabilidad es de
, la probabilidad es de 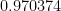 , más del
, más del 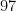 %.
%.
Para 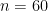 , la probabilidad es de
, la probabilidad es de 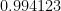 , ¡¡más del
, ¡¡más del 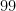 %!!.
%!!.
La cuestión es que generalmente cada persona tiende a imaginar la probabilidad de que, partiendo de una persona concreta, haya otra que coincida en cumpleaños con ella. La probabilidad de ésto es muy baja con 23 personas. La clave del tema es que hay multitud de posibles parejas que pueden formarse conforme vamos aumentando el número de personas del grupo. Por eso la probabilidad acaba siendo tan alta en un grupo tan pequeño.
Graxias (y demostración matemática): Gaussianos
 ), etc... son relativamente modernos. En el siglo XVII, por ejemplo, aún se usaban las letras p de plus para la suma, m de minus para la resta... La raíz cuadrada se expresaba como R.q. y la cúbica como R.c.
), etc... son relativamente modernos. En el siglo XVII, por ejemplo, aún se usaban las letras p de plus para la suma, m de minus para la resta... La raíz cuadrada se expresaba como R.q. y la cúbica como R.c.